Patterned Environments

Until now most studies have concentrated on the behavior of microswimmers in homogeneous environments, where one typically observes a crossover from ballistic motion at short times to enhanced diffusion at long times, the latter due to random changes in the swimming direction. However, self-propelled particles often move in patterned environments, e.g., inside the intestinal tract, which provides the natural habitat of E. coli, or during bioremediation, where chemotactic bacteria spread through porous polluted soils. In a similar fashion, artificial microswimmers must also reliably perform their tasks in complex surroundings, e.g., inside lab-on-a chip devices or living organisms.

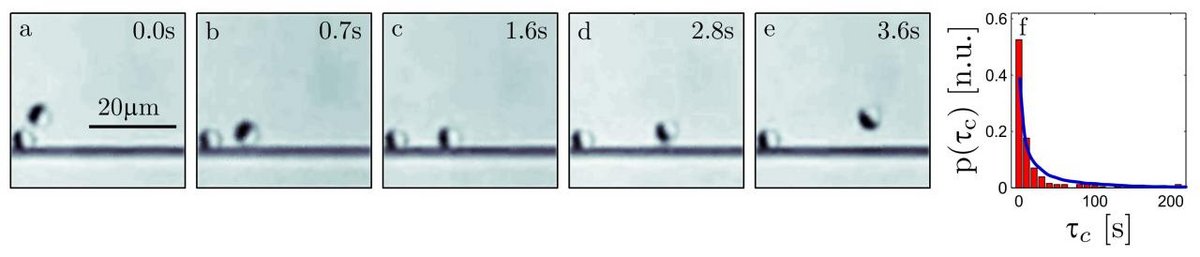
As a first step towards more realistic conditions under which such microswimmers are found and will be employed, we study their behavior in patterned surroundings where frequent encounters with obstacles become important. In particular, we investigate their motion within environments featuring simple topographical structures such as a straight wall, a pore, and periodically arranged obstacles. In order to perform such experiments, we also develop a new species of artiffical microswimmers featuring a tunable active Brownian motion.

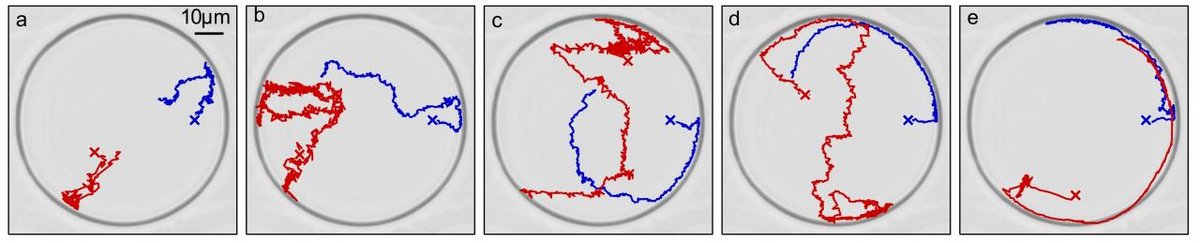
When self-propelled particles swim through a patterned medium, in particular for high swimming velocities, frequent encounters with obstacles will occur. In a typical particle-obstacle encounter, first the particle approaches the wall and gets in contact. Then it slides along the wall until rotational diffusion realigns the particle so that its orientation points away from the wall and leads to particle detachment. When an active particle is confined inside a pore, the chances that it encounters the cavity wall in one of its straight runs increase as the average length of the directed segments become larger. Once the particle touches the wall, it starts diffusing along the cavity perimeter until the rotational diffusion orients the cap towards the interior of the well. This obviously affects the particle distribution, which deviates from the equilibrium distribution.

Sorting of Microswimmers

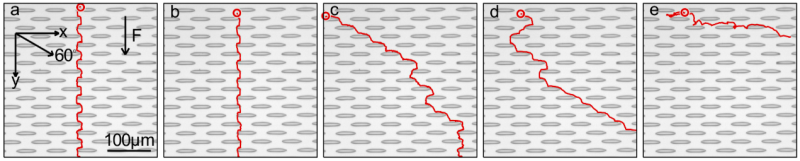
We have also investigated the behavior of self-propelled particles in the presence of a two-dimensional periodic pattern where straight unlimited swims are only possible along certain directions. This leads to strong differences in the particle trajectories depending on their swimming length. In the presence of an additionally applied drift force, this permits us to separate the microswimmers according to their swimming behaviour.