Novel TIRM

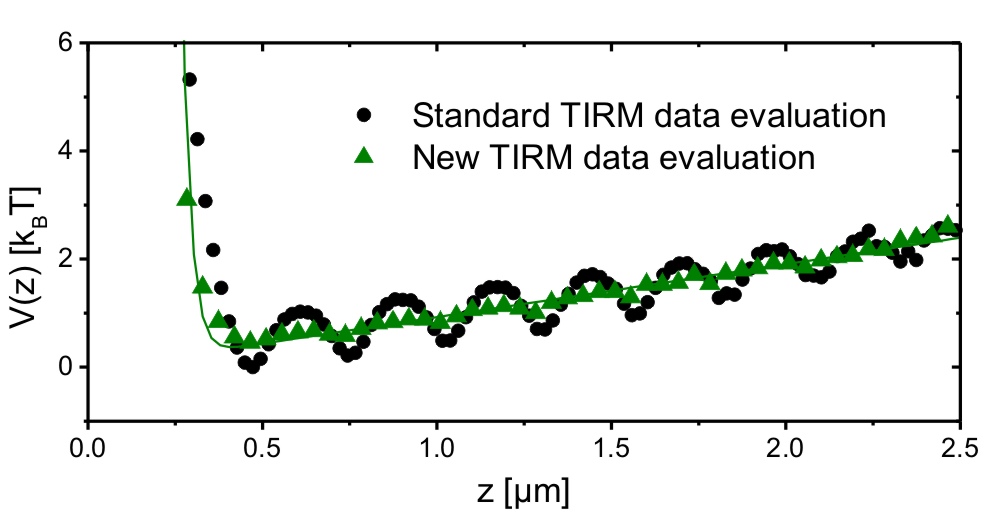
The fact that standard TIRM relies on the a priori knowledge of I(z) poses considerable constraints to the experimental conditions where TIRM can be applied. Besides metallic surfaces which can be easily functionalized with SAMs and hence are interesting for biological purposes, this also affects measurements with high penetration depths which offer the possibility to look further into the medium. Thus a method to in situ determine the correct I(z) without any assumptions on the shape is highly desirable.
Indeed this is possible by utilizing additional information about the system:

1. Between the particle and the wall there is a hydrodynamic interaction leading to a distant dependent friction and hence a reduced diffusivity if the particle approaches the wall. The resulting distance dependence of the diffusion coefficient D(z) is well described theoretically by the “Brenner-formula” which has been established in 1961 and has been proven to be correct several times.
2. As Brownian motion is a gaussian stochastic process, the propagator p(Δz;z0, Δt) giving the probability of a Brownian increment Δz within a time step Δt, starting at a certain position z0 is perfectly symmetric for sufficiently small time steps Δt.

Given the trajectory z(t) of the particle, it is possible to calculate p(Δz;z0, Δt) and D(z) experimentally.
The algorithm’s basic idea can be summarized as follows:

• Guess an I(z) and determine the putative trajectory z(t).
• Calculate p(Δz;z0, Δt) and D(z) and check if the conditions resulting from 1. and 2. are satisfied.
• Try with modified I(z) until the conditions are fulfilled.

The resulting I(z) can be used to calculate high precision trajectories z(t) on metallic surfaces, high penetration depths and s-polarization to determine the forces between particle and wall or to study Brownian dynamics. Furthermore this technique can be used to double-check standard TIRM measurements or even to automatize the whole TIRM data evaluation process, maybe providing the missing link to a widespread use of TIRM in other fields like biology where autonomous evaluation procedures are highly appreciated.