Properties of nonlinear baths

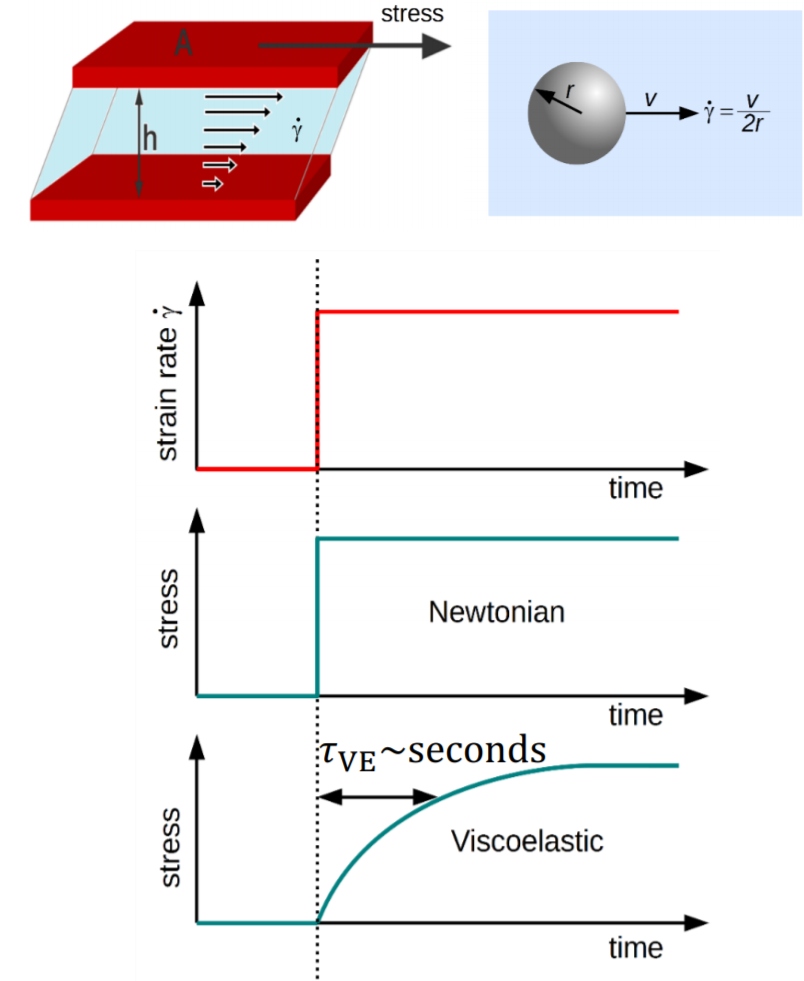
A colloidal particle is a prominent example of a stochastic system, and, if suspended in a simple viscous liquid, very closely resembles the case of an ideal random walker. A variety of new phenomena have been observed when such colloid is suspended in a viscoelastic fluid instead, for example pronounced nonlinear responses when the viscoelastic bath is driven out of equilibrium. Here, using a micron-sized particle in a micellar solution, we investigate in detail, how these nonlinear bath properties leave their fingerprints already in equilibrium measurements, for the cases where the particle is unconfined or trapped in a harmonic potential. We find that the coefficients in an effective linear (generalized) Langevin equation show intriguing inter-dependencies, which can be shown to arise only in nonlinear baths: for example, the friction memory can depend on the external potential that acts only on the colloidal particle, it can depend on the mass of the colloid, or, in an overdamped setting, on its bare diffusivity. These inter-dependencies, caused by so-called fluctuation renormalizations, are seen in an exact small time expansion of the friction memory based on microscopic starting points. Using linear response theory, they can be interpreted in terms of microrheological modes of force-controlled or velocity-controlled driving. The mentioned nonlinear markers are observed in our experiments, which are astonishingly well reproduced by a stochastic Prandtl–Tomlinson model mimicking the nonlinear viscoelastic bath. The pronounced nonlinearities seen in our experiments together with the good understanding in a simple theoretical model make this system a promising candidate for exploration of colloidal motion in nonlinear stochastic environments.

We experimentally and theoretically investigate the clean and rich system of a Brownian particle suspended in a complex, viscoelastic bath, which indeed shows unexplained non-equilibrium properties. For example, the transient dynamics of a probe particle that has strongly perturbed its surrounding requires a theoretical description to account correctly for the stress release in the strained fluid, which is not yet avaliable.

Combining experimental measurements, analytical computations, and simulations of a stochastic Prandtl–Tomlinson model, we investigated several equilibrium-properties of a colloidal particle suspended in a nonlinear bath. Additionally to displacements being non-Gaussian, a nonlinear bath shows up by unexpected properties of the coefficients of a linearized equation; For example, in a nonlinear bath, the effective friction memory of the bath can depend on the stiffness of a potential trapping the particle, as has been observed in molecular simulations, or on the mass or bare friction of the colloidal particle. These dependencies are observed in our experiments, so that the friction memory of the trapped particle varies by more than a factor of two for different trap stiffness. The mentioned dependencies are also demonstrated in an exact analytic expansion of the memory kernel for small times, for the case of Hamilton and Brownian dynamics.

Colloidal motion in viscoelastic baths, here exemplified by a micellar suspension, provide a new paradigmatic case of stochastic motion, with various phenomena that go far beyond the well-studied cases of colloids in pure solvents. It is thus important to develop basic understanding of such systems, and the studies performed here provide a first step towards systematic investigation and modeling. With the given findings at hand, future work will address non-equilibrium cases, and investigate how the equilibrium observations and modeling will determine nonlinear responses and far from equilibrium properties.