Motion of Asymmetric Particles

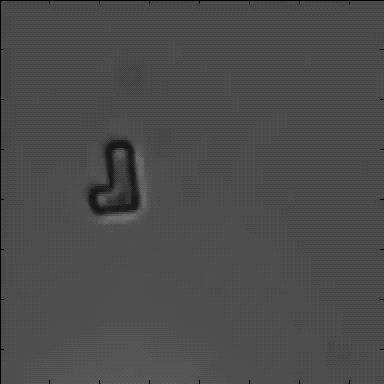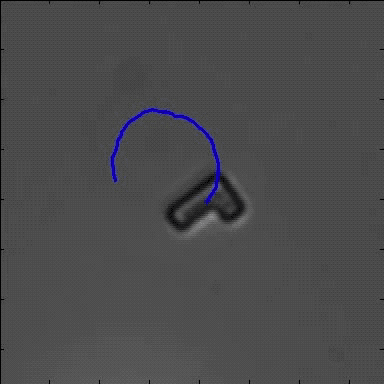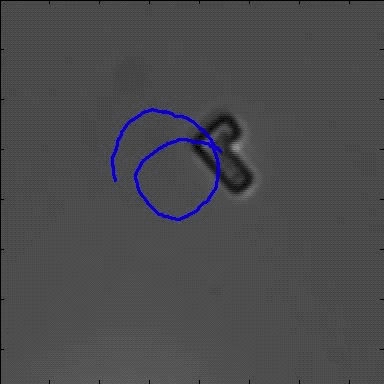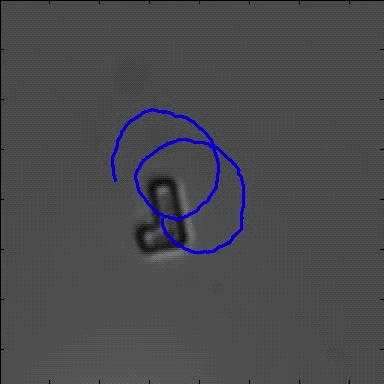
Most systems which have been recently presented in the field of active Brownian motion considered particles with a spherical, cylindrical or elliptical symmetry. However, in contrast to such systems, many biological swimmers (e.g. Paramecium and Chlamydomonas) have a characteristic asymmetry generating a variety of new features. In order to address such aspects, here we focus on the properties of asymmetric self-propelled objects with an L-shape. In agreement with former experiments, those objects are driven by a light induced local chemical gradient being created inside a critical water-2,6-lutidine solution. The driving force acts perpendicular to a gold cap being located at the bottom of the L-particle’s short arm. On moving relative to the surrounding liquid, such particles experience an intrinsic, velocity dependent torque due to the viscous friction. We therefore observe circular trajectories whose orientation depends on the chirality of the swimmer. Owing to the linear relationship between the driving force and the torque, the radius of the circle is constant and only depends on the geometrical properties of the swimmer. 

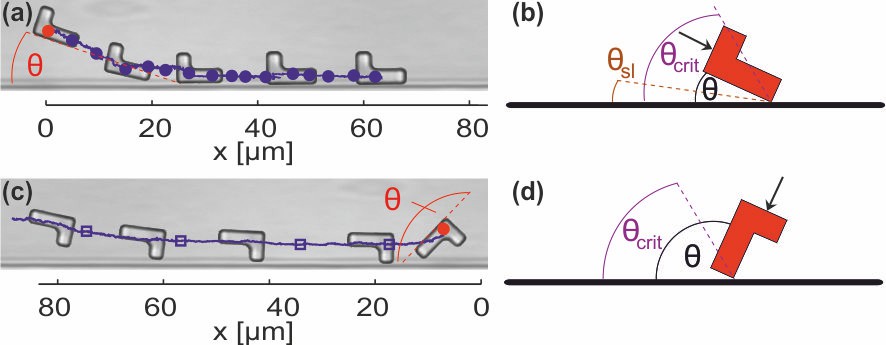
In addition to the bulk conditions, we investigate this particle motion close to straight walls. Depending on the incidence angle and the direction of the torque, there is either a reflection from the wall or a stable sliding along the wall.

Circular motion of L-shaped particles